Value-based methods for deep RL

-
Q-learning:
- The Q-learning algorithm uses Bellman equation to get the unique solution $Q^{*}(s,a)$: $$Q ^ { * } ( s , a ) = ( \mathcal { B } Q ^ { * } ) ( s , a )$$ where $\mathcal{B}$ is the Bellman operator mapping any function $K : \mathcal { S } \times \mathcal { A } arrow \mathbb { R }$ into another function $\mathcal { S } \times \mathcal { A } arrow \mathbb { R }$, defined as follows: $$( \mathcal { B } K ) ( s , a ) = \sum _ { s ^ { \prime } \in S } P ( s , a , s ^ { \prime } ) ( R ( s , a , s ^ { \prime } ) + \gamma \max _ { a ^ { \prime } \in \mathcal { A } } K ( s ^ { \prime } , a ^ { \prime } ) )$$
- By Banach’s theorem, the fixed point of the Bellman operator $\mathcal{B}$ exists since it is a contraction mapping. So Q-learning algorithm can learn the optimal Q-value function. In practice, one general proof of convergence to the optimal value function is available (Watkins and Dayan, 1992) under the conditions that:
- the state-action pairs are represented discretely,
- all actions are repeatedly sampled in all states (which ensures sufficient exploration, hence not requiring access to the transition model).
-
Fitted Q-learning:
- In fitted Q-learning, the algorithm starts with some random initialization of the Q-values $Q(s, a; \theta _ {0})$ where $\theta _ {0}$ refers to the initial parameters. Then, an approximation of the Q-values at the $k$th iteration $Q(s, a; \theta _ {k})$ is updated towards the target value: $$Y _ { k } ^ { Q } = r + \gamma \max _ { a ^ { \prime } \in \mathcal { A } } Q ( s ^ { \prime } , a ^ { \prime } ; \theta _ { k } )$$ where $\theta _ {k}$ refers to some parameters that define the Q-values at the $k$th iteration.
- In neural fitted Q-learning (NFQ), the Q-values are parameterized with a neural network $Q(s, a; \theta _ {k})$ where the parameters $\theta _ {k}$ are updated by stochastic gradient descent by minimizing the square loss: $$\mathrm { L } _ { D Q N } = ( Q ( s , a ; \theta _ { k } ) - Y _ { k } ^ { Q } ) ^ { 2 }$$ The parameters are updated as: $$\theta _ { k + 1 } = \theta _ { k } + \alpha ( Y _ { k } ^ { Q } - Q ( s , a ; \theta _ { k } ) ) \nabla _ { \theta _ { k } } Q ( s , a ; \theta _ { k } )$$ where $\alpha$ is a scalar step size called the learning rate. Notice that when updating the weights, one also changes the target. Also, Q-values tend to be overestimated due to the max operator.
-
Deep Q-networks:
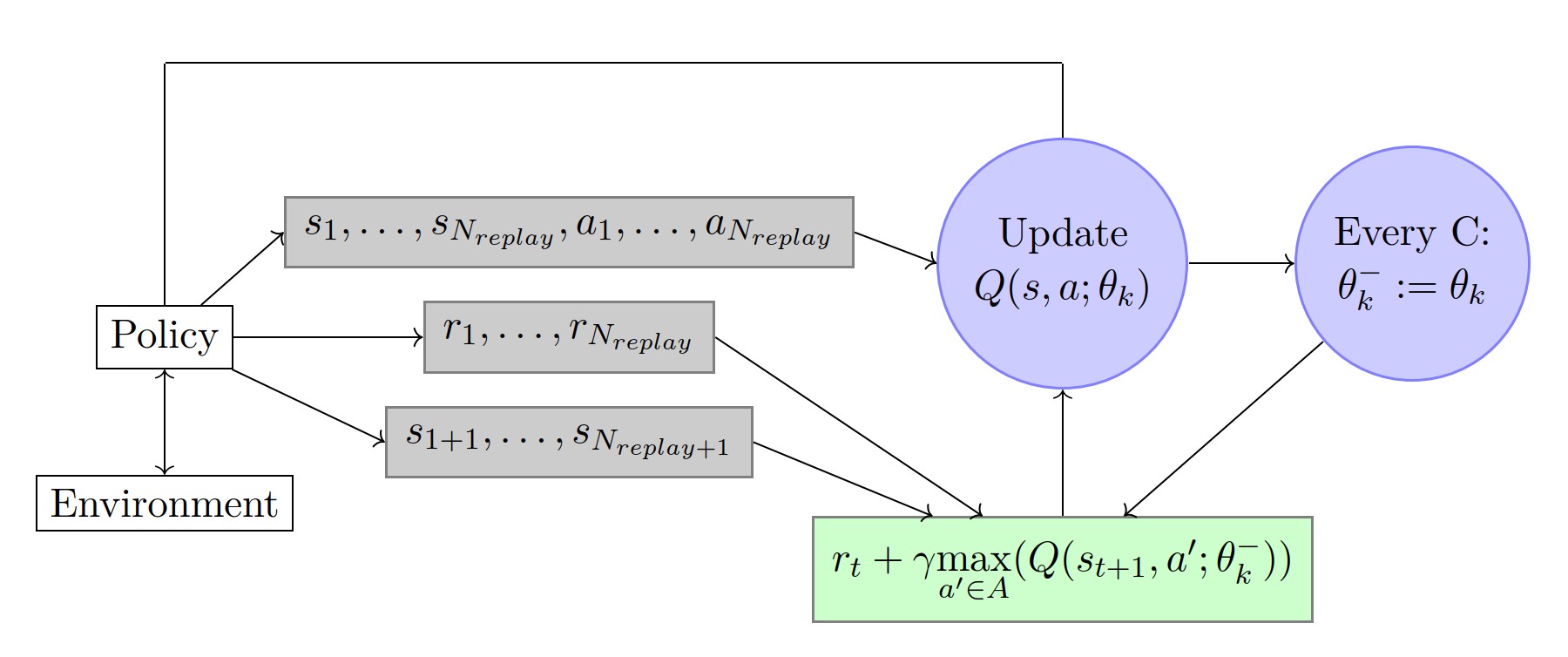
- Similar to fitted Q-learning, the target Q-network is: $$Y _ { k } ^ { Q } = r + \gamma \max _ { a ^ { \prime } \in \mathcal { A } } Q ( s ^ { \prime } , a ^ { \prime } ; \theta _ {k} ^ {-})$$ where $\theta _ { k } ^ { - }$ are updated only every $C \in \mathbb { N }$ iterations with the following assignment: $\theta _ { k } ^ { - } = \theta _ { k }$. This prevents the instabilities to propagate quickly and it reduces the risk of divergence as the target values $Y _ { k } ^ { Q }$ are kept fixed for $C$ iterations.
- In an online setting, the replay memory keeps all information for the last $N _ {replay} \in \mathbb{N}$ time steps. The updates are then made on a set of tuples $<s,a,r,s ^ {\prime} >$ (called mini-batch) selected randomly within the replay memory. This allows for updates that cover a wide range of the state-action space. In addition, one mini-batch update has less variance compared to a single tuple update.
- To keep the target values in a reasonable scale and to ensure proper learning in practice, rewards are clipped between -1 and +1. Clipping the rewards limits the scale of the error derivatives and makes it easier to use the same learning rate across multiple games (however, it introduces a bias).
-
Double DQN:
- The max operation in Q-learning uses the same values both to select and to evaluate an action. This makes it more likely to select overestimated values in case of inaccuracies or noise, resulting in overoptimistic value estimates. Therefore, the DQN algorithm induces an upward bias. The double estimator method uses two estimates for each variable, which allows for the selection of an estimator and its value to be uncoupled (Hasselt, 2010). This allows for the removal of the positive bias in estimating the action values.
- In Double DQN, or DDQN, the target value $Y _ {k} ^ {Q}$ is replaced by: $$Y _ {k} ^ {DDQN} = r + \gamma Q ( s ^ { \prime } , \underset { a \in \mathcal { A } } { \operatorname { argmax } } Q ( s ^ { \prime } , a ; \theta _ { k } ) ; \theta _ { k } ^ { - })$$ which leads to less overestimation of the Q-learning values, as well as improved stability, hence improved performance. Note that the policy is still chosen according to the values obtained by the current weights $\theta$.
- How about triple DQN or $N$ DQN? Possbile research project.
-
Dueling network architecture:
-
The dueling network architecture decouples the value and advantage function $A ^ {\pi}(s, a)$. The Q-value function is given by: $$Q ( s , a ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } , \theta ^ { ( 3 ) } ) = V ( s ; \theta ^ { ( 1 ) } , \theta ^ { ( 3 ) } )+ ( A ( s , a ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } ) - \max _ { a ^ { \prime } \in \mathcal { A } } A ( s , a ^ { \prime } ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } ) )$$ (Question: why not just Q=V+A?)
For $a ^ { * } = \operatorname { argmax } _ { a ^ { \prime } \in \mathcal { A } } Q ( s , a ^ { \prime } ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } , \theta ^ { ( 3 ) } )$, we have $Q ( s , a ^ { * } ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } , \theta ^ { ( 3 ) } ) = V ( s ; \theta ^ { ( 1 ) } , \theta ^ { ( 3 ) } )$. -
The structure of dueling network:
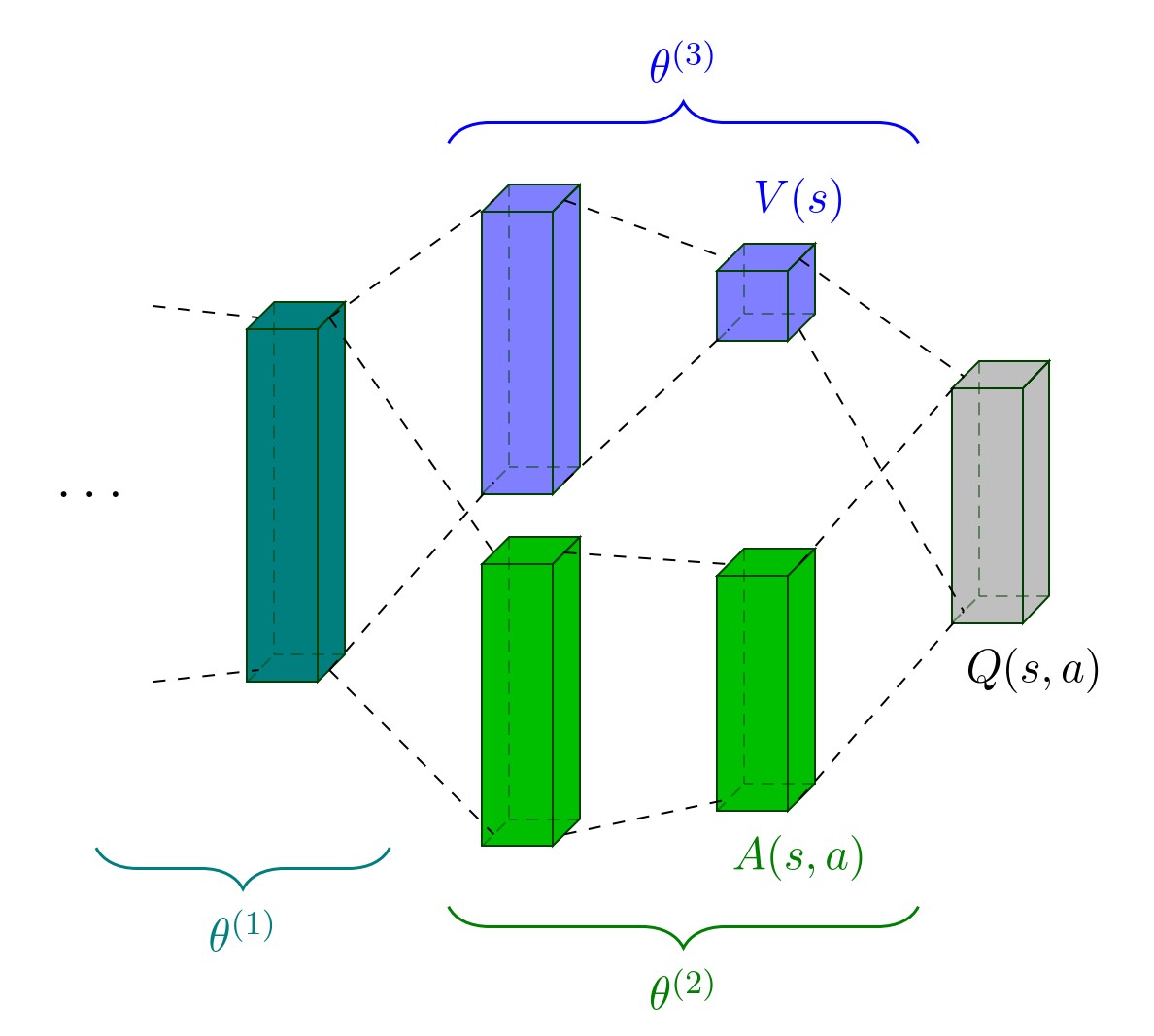
The stream $V( s ; \theta ^ { ( 1 ) } , \theta ^ { ( 3 ) })$ provides an estimate of the value function, while the other stream produces an estimate of the advantage function. The learning update is done as in DQN and it is only the structure of the neural network that is modified.
-
A slightly different approach is preferred in practice because it increases the stability of the optimization: $$Q ( s , a ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } , \theta ^ { ( 3 ) } ) = V ( s ; \theta ^ { ( 1 ) } , \theta ^ { ( 3 ) } ) + ( A ( s , a ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } ) - \frac { 1 } { | \mathcal { A } | } \sum _ { a ^ { \prime } \in \mathcal { A } } A ( s , a ^ { \prime } ; \theta ^ { ( 1 ) } , \theta ^ { ( 2 ) } ) )$$ In that case, the advantages only need to change as fast as the mean, which appears to work better in practice.
-
-
Distributional DQN:
-
Another approach is to aim for a richer representation through a value distribution, i.e. the distribution of possible cumulative returns. This value distribution provides more complete information of the intrinsic randomness of the rewards and transitions of the agent within its environment (note that it is not a measure of the agent’s uncertainty about the environment).
-
The value distribution $Z ^ {\pi}$ is a mapping from state-action pairs to distributions of returns when following policy $\pi$. It has an expectation equal to $Q ^ {\pi}$: $$Q ^ { \pi } ( s , a ) = \mathbb { E } [ Z ^ { \pi } ( s , a ) ]$$ This random return is also described by a recursive equation:
$$Z ^ { \pi } ( s , a ) = R ( s , a , S ^ { \prime } ) + \gamma Z ^ { \pi } ( S ^ { \prime } , A ^ { \prime } )$$ where we use capital letters to emphasize the random nature of the next state-action pair $(S ^ {\prime}, A ^ {\prime})$ and $A ^ { \prime } \sim \pi ( \cdot | S ^ { \prime } )$. -
This approach has two main advantages: 1. It is possible to implement risk-aware behavior. 2. It leads to more performant learning in practice. The distributional perspective naturally provides a richer set of training signals than a scalar value function $Q(s,a)$. These training signals that are not a priori necessary for optimizing the expected return are known as auxiliary tasks and lead to an improved learning.
-
-
Multi-step learning:
- Non-bootstrapping methods learn directly from returns (Monte Carlo) and an intermediate solution is to use a multi-step target. Such a variant in the case of DQN can be obtained by using the n-step target value given by: $$Y _ { k } ^ { Q , n } = \sum _ { t = 0 } ^ { n - 1 } \gamma ^ { t } r _ { t } + \gamma ^ { n } \max _ { a ^ { \prime } \in A } Q ( s _ { n } , a ^ { \prime } ; \theta _ { k } )$$ where $( s _ { 0 } , a _ { 0 } , r _ { 0 } , \cdots , s _ { n - 1 } , a _ { n - 1 } , r _ { n - 1 } , s _ { n })$ is any trajectory of $n+1$ time steps with $s = s _ 0$ and $a = a _ 0$.
- A combination of different multi-steps targets can also be used: $$Y _ { k } ^ { Q , n } = \sum _ { i = 0 } ^ { n - 1 } \lambda _ { i } ( \sum _ { t = 0 } ^ { i } \gamma ^ { t } r _ { t } + \gamma ^ { i + 1 } \max _ { a ^ { \prime } \in A } Q ( s _ { i + 1 } , a ^ { \prime } ; \theta _ { k } ) )$$ with $\sum _ { i = 0 } ^ { n - 1 } \lambda _ { i } = 1$. In the method called TD($\lambda$), $n \rightarrow \infty$ and $\lambda _ { i }$ follow a geometric law: $\lambda _ { i } \propto \lambda ^ { i }$ where $0 \leq \lambda \leq 1$.
-
Bootstrapping:
- Disadvantage: using pure bootstrapping methods (such as in DQN) are prone to instabilities when combined with function approximation because they make recursive use of their own value estimate at the next time-step. Methods that rely less on bootstrapping can propagate information more quickly from delayed rewards as they learn directly from returns.
- Advantage: using value bootstrap allows learning from off-policy samples. With bootstrapping, most algorithms learn faster.
Policy gradient methods
Stochastic Policy Gradient
-
The expected return of a stochastic policy $\pi$ starting from a given state $s _ 0$: $$V ^ { \pi } \left( s _ { 0 } \right) = \int _ { \mathcal { S } } \rho ^ { \pi } ( s ) \int _ { \mathcal { A } } \pi ( s , a ) R ^ { \prime } ( s , a ) da ds$$ where $R^{\prime}(s, a)=\int_{s^{\prime} \in \mathcal{S}} \operatorname{Pr}\left(s, a, s^{\prime}\right) R\left(s, a, s^{\prime}\right)$ and $\rho \pi (s)$ is the discounted state distribution defined as: $$\rho ^ { \pi } ( s ) = \sum _ { t = 0 } ^ { \infty } \gamma ^ { t } \operatorname {Pr} ( s _ { t } = s | s _ { 0 } , \pi )$$
-
For a differentiable policy $\pi _ w$, the fundamental result underlying these algorithms is the policy gradient theorem: $$\nabla _ { w } V ^ { \pi _ { w } } \left( s _ { 0 } \right) = \int _ { \mathcal { S } } \rho ^ { \pi _ { w } } ( s ) \int _ { \mathcal { A } } \nabla _ { w } \pi _ { w } ( s , a ) Q ^ { \pi _ { w } } ( s , a ) da ds$$ This result allows us to adapt the policy parameters from experience. This result is particularly interesting since the policy gradient does not depend on the gradient of the state distribution (even though one might have expected it to). The REINFORCE algorithm is a simple example.
-
Policy gradient methods should include two steps:
- Policy evaluation: estimates $Q ^ { \pi _ { w } }$.
- Policy improvement: it takes a gradient step to optimize the policy $\pi _ w(s, a)$ with respect to the value function estimation. Intuitively, the policy improvement step increases the probability of the actions proportionally to their expected return.
-
How to obtain an estimate of $Q ^ { \pi _ { w } }$?
- Monte-Carlo policy gradient: it estimates the $Q ^ { \pi _ { w } } (s,a)$ from rollouts on the environment while following policy $\pi _ { w }$. It is unbiased and, without instabilities induced by bootstrapping. However, the estimate requires on-policy rollouts and can exhibit high variance. Several rollouts are typically needed to obtain a good estimate of the return (not sample efficient).
- Actor-critic methods: use an estimate of the return given by a value-based approach, more efficient.
-
Remarks:
- To prevent the policy from becoming deterministic, it is common to add an entropy regularizer to the gradient. With this regularizer, the learnt policy can remain stochastic. This ensures that the policy keeps exploring.
- Advantage value function: While $Q ^ { \pi _ { w } } (s,a)$ summarizes the performance of each action for a given state under policy $\pi _ w$, the advantage function $A ^ { \pi _ { w } } (s,a)$ provides a measure of comparison for each action to the expected return at the state $s$, given by $V ^ { \pi _ { w } } (s)$. Using $A ^ { \pi _ { w } } ( s , a ) = Q ^ { \pi _ { w } } ( s , a ) - V ^ { \pi _ { w } } ( s )$ has usually lower magnitudes than $Q ^ { \pi _ { w } } (s,a)$. This helps reduce the variance of the gradient estimator in the policy improvement step, while not modifying the expectation. The value function $V ^ {{ \pi } _ w} ( s )$ can be seen as a baseline or control variate for the gradient estimator. Using such a baseline allows for improved numerical efficiency – i.e. reaching a given performance with fewer updates – because the learning rate can be bigger.
Deterministic Policy Gradient
- Let us denote by $\pi (s)$ the deterministic policy: $\pi ( s ) : \mathcal { S } \rightarrow \mathcal { A }$. In discrete action spaces, a direct approach is to build the policy iteratively with: $$\pi _ { k + 1 } ( s ) = \underset { a \in \mathcal { A } } { \operatorname { argmax } } Q ^ { \pi _ { k } } ( s , a )$$ where $\pi _ { k }$ is the policy at the $k$th iteration.
- Deep Deterministic Policy Gradient (DDPG): In continuous action spaces, a greedy policy improvement becomes problematic, requiring a global maximization at every step. Instead, let us denote by $\pi _ w ( s )$ a differentiable deterministic policy. In that case, a simple and computationally attractive alternative is to move the policy in the direction of the gradient of $Q$: $$\nabla _ { w } V ^ { \pi _ { w } } \left( s _ { 0 } \right) = \mathbb { E } _ { s \sim \rho ^ { \pi _ { w } } } \left[ \nabla _ { w } \left( \pi _ { w } \right) \nabla _ { a } \left. \left( Q ^ { \pi _ { w } } ( s , a ) \right) \right| _ { a = \pi _ { w } ( s ) } \right]$$ This equation implies relying on $\nabla _ { a } \left( Q ^ { \pi w } ( s , a ) \right)$ (in addition to $\nabla _ { a } \left( Q ^ { \pi w } ( s , a ) \right)$), which usually requires using actor-critic methods.
Actor-Critic Methods
The actor refers to the policy and the critic to the estimate of a value function (e.g., the Q-value function). In deep RL, both the actor and the critic can be represented by non-linear neural network function approximators. The actor uses gradients derived from the policy gradient theorem and adjusts the policy parameters $w$. The critic, parameterized by $\theta$, estimates the approximate value function for the current policy $\pi$.
- The critic:
- TD(0): at every iteration, the current value $Q(s,a;\theta)$ is updated towards a target value: $Y _ { k } ^ { Q } = r + \gamma Q \left( s ^ { \prime } , a = \pi \left( s ^ { \prime } \right) ; \theta \right)$. It is simple yet not computationally efficient as it uses a pure bootstrapping technique that is prone to instabilities and has a slow reward propagation backwards in time.
- Retrace ($\lambda$): (i) it can make use of samples collected from any behavior policy without introducing a bias and (ii) it is efficient as it makes the best use of samples collected from near on-policy behavior policies. These architectures are sample-efficient thanks to the use of a replay memory, and computationally efficient since they use multi-step returns which improves the stability of learning and increases the speed of reward propagation backwards in time.
- The actor: the off-policy gradient in the policy improvement phase for the stochastic case is given as:
$$\nabla _ { w } V ^ { \pi _ { w } } \left( s _ { 0 } \right) = \mathbb { E } _ { s \sim \rho ^ { \pi _ { \beta } } , a \sim \pi _ { \beta } } \left[ \nabla _ { \theta } \left( \log \pi _ { w } ( s , a ) \right) Q ^ { \pi _ { w } } ( s , a ) \right]$$
where $\beta$ is a behavior policy generally different than $\pi$, which makes the gradient generally biased.
- In the case of actor-critic methods, an approach to perform the policy gradient on-policy without experience replay has been investigated with the use of asynchronous methods, where multiple agents are executed in parallel and the actor-learners are trained asynchronously. The parallelization of agents also ensures that each agent experiences different parts of the environment at a given time step. In that case, n-step returns can be used without introducing a bias. It removes the need to maintain a replay buffer. However, it is not sample efficient.
- An alternative is to combine off-policy and on-policy samples to trade-off both the sample efficiency of off-policy methods and the stability of on-policy gradient estimates. For example, Q-Prop uses a Monte Carlo on-policy gradient estimator, while reducing the variance of the gradient estimator by using an off-policy critic as a control variate. One limitation of Q-Prop is that it requires using on-policy samples for estimating the policy gradient.
Natural Policy Gradients
- Natural policy gradient methods use the steepest direction given by the Fisher information metric, i.e. the update follows the direction that maximizes $( J ( w ) - J ( w + \Delta w ) )$ under a constraint on $| \Delta w | _ { 2 }$.
- In the hypothesis that the constraint on $\Delta w$ is defined with another metric than $L _ 2$, the first-order solution to the constrained optimization problem typically has the form $\Delta w \propto B ^ { - 1 } \nabla _ { w } J ( w )$ where B is an $n _ w \times n _ w$ matrix.
- In natural gradients, the norm uses the Fisher information metric, given by a local quadratic approximation to the KL divergence $D _ {KL} \left( \pi ^ { w } | \pi ^ { w + \Delta w } \right)$. The natural gradient ascent for improving the policy π w is given by: $$\Delta w \propto F _ { w } ^ { - 1 } \nabla _ { w } V ^ { \pi _ { w } } ( \cdot )$$ where $F _ { w }$ is the Fisher information matrix given by: $$F _ { w } = \mathbb { E } _ { \pi _ { w } } \left[ \nabla _ { w } \log \pi _ { w } ( s , \cdot ) \left( \nabla _ { w } \log \pi _ { w } ( s , \cdot ) \right) ^ { T } \right]$$
- As the angle between natural and ordinary gradient is never larger than ninety degrees, convergence is also guaranteed when using natural gradients. In the case of neural networks and their large number of parameters, it is usually impractical to compute, invert, and store the Fisher information matrix.
Trust Region Optimization
- The policy optimization methods based on trust region restrict the changes in a policy using the KL divergence between the action distributions. By bounding the size of the policy update, trust region methods also bound the changes in state distributions guaranteeing improvements in policy.
- Trust Region Policy Optimization (TRPO): uses constrained updates and advantage function estimation to perform the update, resulting in the reformulated optimization given by $$\max _ { \Delta w } \mathbb { E } _ { s \sim \rho ^ { \pi } w , a \sim \pi } \left[ \frac { \pi _ { w + \Delta w } ( s , a ) } { \pi _ { w } ( s , a ) } A ^ { \pi _ w } ( s , a ) \right]$$ subject to $\mathbb { E }[ D _ { \mathrm { KL } } \left( \pi _ { w } ( s , \cdot ) | \pi _ { w + \Delta w } ( s , \cdot ) \right) ] \leq \delta$, where $\delta \in \mathbb{R}$ is a hyperparameter.
- Proximal Policy Optimization (PPO): it is a variant of the TRPO algorithm, which formulates the constraint as a penalty or a clipping objective, instead of using the KL constraint. PPO considers modifying the objective function to penalize changes to the policy that move r t ( w ) = π w+4w (s,a) π w (s,a) away from 1. The clipping objective that PPO maximizes is given by: $$\underset { s \sim \rho ^ { \pi } w , a \sim \pi _ { w } } { \mathbb { E } } \left[ \min \left( r _ { t } ( w ) A ^ { \pi _ { w } } ( s , a ) , \operatorname { clip } \left( r _ { t } ( w ) , 1 - \epsilon , 1 + \epsilon \right) A ^ { \pi _ { w } } ( s , a ) \right) \right]$$ where $\epsilon \in \mathbb{R}$ is a hyperparameter. This objective function clips the probability ratio to constrain the changes of $r _ t$ in the interval $[1− \epsilon, 1+ \epsilon]$.
Combining policy gradient and Q-learning
- Policy gradient algorithms have the following properties unlike the methods based on DQN:
- They are able to work with continuous action spaces. This is particularly interesting in applications such as robotics, where forces and torques can take a continuum of values.
- They can represent stochastic policies, which is useful for building policies that can explicitly explore. This is also useful in settings where the optimal policy is a stochastic policy (e.g., in a multi-agent setting where the Nash equilibrium is a stochastic policy).
- Combine policy gradient methods directly with off-policy Q-learning: In some specific settings, depending on the loss function and the entropy regularization used, value-based methods and policy-based methods are equivalent. For instance, when adding an entropy regularization, we have: $$\nabla _ { w } V ^ { \pi _ { w } } \left( s _ { 0 } \right) = \mathbb { E } _ { s , a } \left[ \nabla _ { w } \left( \log \pi _ { w } ( s , a ) \right) Q ^ { \pi _ { w } } ( s , a ) \right] + \alpha \mathbb { E } _ { s } [ \nabla _ { w } H ^ { \pi _ { w } } ( s )]$$ where $H ^ { \pi } ( s ) = - \sum _ { a } \pi ( s , a ) \log \pi ( s , a )$. From this, one can note that an optimum is satisfied by the following policy: $\pi _ { w } ( s , a ) = \exp ( \frac{A ^ { \pi _ w } ( s , a )}{\alpha} - H ^ { \pi _ w } ( s ) )$. Therefore, we can use the policy to derive an estimate of the advantage function: $$\tilde { A } ^ { \pi _ { w } } ( s , a ) = \alpha \left( \log \pi _ { w } ( s , a ) + H ^ { \pi } ( s ) \right)$$
- Both value-based and policy-based methods are model-free and they do not make use of any model of the environment.
Model-based methods
Pure model-based methods: When a model of the environment is available, planning consists in interacting with the model to recommend an action. In the case of discrete actions, lookahead search is usually done by generating potential trajectories. In the case of a continuous action space, trajectory optimization with a variety of controllers can be used.
- Lookahead search: limited to discrete actions
- A lookahead search in an MDP iteratively builds a decision tree where the current state is the root node. It stores the obtained returns in the nodes and focuses attention on promising potential trajectories.
- Monte-Carlo tree search (MCTS): The idea is to sample multiple trajectories from the current state until a terminal condition is reached (e.g., a given maximum depth). From those simulation steps, the MCTS algorithm then recommends an action to take.
- Recent works have developed strategies to directly learn end-to-end the model, along with how to make the best use of it, without relying on explicit tree search techniques. These approaches show improved sample efficiency, performance, and robustness to model misspecification compared to the separated approach (simply learning the model and then relying on it during planning). Why?
- Trajectory optimization:
- If the model is differentiable, one can directly compute an analytic policy gradient by backpropagation of rewards along trajectories. For instance, PILCO uses Gaussian processes to learn a probabilistic model of the dynamics. It can then explicitly use the uncertainty for planning and policy evaluation in order to achieve a good sample efficiency. However, the gaussian processes have not been able to scale reliably to high-dimensional problems.
- Wahlström et al. (2015) uses a deep learning model of the dynamics (with an auto-encoder) along with a model in a latent state space. Model-predictive control (Morari and Lee, 1999) can then be used to find the policy by repeatedly solving a finite-horizon optimal control problem in the latent space.
- Watter et al. (2015) builds a probabilistic generative model in a latent space with the objective that it possesses a locally linear dynamics, which allows control to be performed more efficiently.
- Another approach is to use the trajectory optimizer as a teacher rather than a demonstrator: guided policy search takes a few sequences of actions suggested by another controller. It then learns to adjust the policy from these sequences.
Integrating model-free and model-based methods: the respective strengths of the model-free versus model-based approaches depend on different factors.
- The best suited approach depends on whether the agent has access to a model of the environment. If that’s not the case, the learned model usually has some inaccuracies that should be taken into account.
- A model-based approach requires working in conjunction with a planning algorithm (or controller), which is often computationally demanding. The time constraints for computing the policy $\pi (s)$ via planning must therefore be taken into account (e.g., for applications with real-time decision-making or simply due to resource limitations).
- For some tasks, the structure of the policy (or value function) is the easiest one to learn, but for other tasks, the model of the environment may be learned more efficiently due to the particular structure of the task (less complex or with more regularity). Thus, the most performant approach depends on the structure of the model, policy, and value function.
How to obtain advantages from both worlds by integrating learning and planning:
- When the model is available, one direct approach is to use tree search techniques that make use of both value and policy networks.
- When the model is not available and under the assumption that the agent has only access to a limited number of trajectories, the key property is to have an algorithm that generalizes well. One possibility is to build a model that is used to generate additional samples for a model-free reinforcement learning algorithm. Another possibility is to use a model-based approach along with a controller such as MPC to perform basic tasks and use model-free fine-tuning in order to achieve task success.
- Other approaches build neural network architectures that combine both model-free and model-based elements. The VIN architecture (Tamar et al., 2016) is a fully differentiable neural network with a planning module that learns to plan from model-free objectives (given by a value function). It works well for tasks that involve planning-based reasoning (navigation tasks) from one initial position to one goal position and it demonstrates strong generalization in a few different domains.
Improving the combination of model-free and model-based ideas is one key area of research for the future development of deep RL algorithms.
Generalization
Generalization refers to either
- the capacity to achieve good performance in an environment where limited data has been gathered, or
- the capacity to obtain good performance in a related environment.
In the former case, the idea of generalization is directly related to the notion of sample efficiency (e.g., when the state-action space is too large to be fully visited). In the latter case, the test environment has common patterns with the training environment but can differ in the dynamics and the rewards. For instance, the underlying dynamics may be the same but a transformation on the observations may have happened.
Let us consider the case of a finite dataset $D$ obtained on the exact same task as the test environment. Formally, a dataset available to the agent $D \sim D$ can be defined as a set of four-tuples $(s, a, r, s^{\prime}) \in S \times A \times R \times S$ gathered by sampling independently and identically (i.i.d.).
- a given number of state-action pairs $(s,a)$ from some fixed distribution with $P(s, a)>0$, $\forall (s,a) \in S \times A$;
- a next state $s ^ {\prime} \sim P(s, a, \cdot)$;
- a reward $r = R(s, a, s ^ {\prime})$; We denote by $D _ {\infty}$ the particular case of a dataset $D$ where the number of tuples tends to infinity.
A learning algorithm can be seen as a mapping of a dataset $D$ into a policy $\pi _ D$. Then we can decompose the suboptimality of the expected return as follows:
$$\underset { D \sim \mathcal { D } } { \mathbb { E } } [ V ^ { \pi ^ { * } } ( s ) - V ^ { \pi _ { D } } ( s ) ]$$ $$= \underset { D \sim \mathcal { D } } { \mathbb { E } } [ V ^ { \pi ^ { * } } ( s ) - V ^ { \pi _ { D \infty } } ( s ) + V ^ { \pi _ { D \infty } ( s ) } - V ^ { \pi _ { D } } ( s ) ]$$ $$ = \underbrace { ( V ^ { \pi ^ { * } } ( s ) - {V ^ { \pi _ { D _ { \infty } } } ( s ) ) } } _ { \text {asymptotic bias} } + \underbrace { \underset { D \sim \mathcal { D } } { \mathbb { E } } [ { V ^ { \pi _ { D \infty } } ( s ) } - V ^ { \pi _ { D } } ( s ) ] } _ { \text {error due to finite size of the dataset } D } $$
This decomposition highlights two different terms: (i) an asymptotic bias which is independent of the quantity of data and (ii) an overfitting term directly related to the fact that the amount of data is limited.
Improving generalization can be seen as a tradeoff between (i) an error due to the fact that the algorithm trusts completely the frequentist assumption (i.e., discards any uncertainty on the limited data distribution) and (ii) an error due to the bias introduced to reduce the risk of overfitting. When the quality of the dataset is low, the learning algorithm should favor more robust policies (i.e., consider a smaller class of policies with stronger generalization capabilities). When the quality of the dataset increases, the risk of overfitting is lower and the learning algorithm can trust the data more, hence reducing the asymptotic bias.
We discuss the following key elements that are at stake when one wants to improve generalization in deep RL:
- the state representation;
- the learning algorithm (type of function approximator, model-free vs model-based);
- the objective function (e.g., reward shaping, tuning the training discount factor);
- using hierarchical learning.
Different aspects that can be used to avoid overfitting to limited data.
- Feature selection: The appropriate level of abstraction plays a key role in the bias-overfitting tradeoff and one of the key advantages of using a small but rich abstract representation is to allow for improved generalization.
- Overfitting: When considering many features on which to base the policy, an RL algorithm may take into consideration spurious correlations, which leads to overfitting.
- Asymptotic bias: Removing features that discriminate states with a very different role in the dynamics introduces an asymptotic bias. The same policy would be enforced on undistinguishable states, hence leading to a sub-optimal policy.
- In deep RL, one approach is to first infer a factorized set of generative factors from the observations. This can be done for instance with an encoder-decoder architecture variant. These features can then be used as inputs to a reinforcement learning algorithm. The learned representation can, in some contexts, greatly help for generalization as it provides a more succinct representation that is less prone to overfitting. Some features may be kept in the abstract representation because they are important for the reconstruction of the observations, though they are otherwise irrelevant for the task at hand. Crucial information about the scene may also be discarded in the latent representation, particularly if that information takes up a small proportion of the observations $x$ in pixel space.
- Learning algorithm and function approximator selection:
- If the function approximator used for the value function and/or the policy and/or the model is too simple, an asymptotic bias may appear. When the function approximator has poor generalization, there will be a large error due to the finite size of the dataset (overfitting).
- One approach to mitigate non-informative features is to force the agent to acquire a set of symbolic rules adapted to the task and to reason on a more abstract level. This abstract level reasoning and the improved generalization have the potential to induce high-level cognitive functions such as transfer learning and analogical reasoning. For instance, the function approximator may embed a relational learning structure and thus build on the idea of relational reinforcement learning.
- Auxiliary tasks: In the context of deep reinforcement learning, Jaderberg et al. (2016) show that augmenting a deep reinforcement learning agent with auxiliary tasks within a jointly learned representation can drastically improve sample efficiency in learning. This is done by maximizing simultaneously many pseudo-reward functions. The argument is that learning related tasks introduces an inductive bias that causes a model to build features in the neural network that are useful for the range of tasks. By explicitly learning both the model-free and model-based components through the state representation, along with an approximate entropy maximization penalty, the CRAR agent (François-Lavet et al., 2018) shows how it is possible to learn a low-dimensional representation of the task. In addition, this approach can directly make use of a combination of model-free and model-based, with planning happening in a smaller latent state space.
Modifying the objective function
In order to improve the policy learned by a deep RL algorithm, one can optimize an objective function that diverts from the actual objective. By doing so, a bias is usually introduced but this can in some cases help with generalization.
- Reward shaping: In practice, reward shaping uses prior knowledge by giving intermediate rewards for actions that lead to desired outcome. It is usually formalized as a function $F(s, a, s ^ {\prime})$ added to the original reward function $R(s, a, s ^ {\prime})$ of the original MDP. This technique is often used in deep reinforcement learning to improve the learning process in settings with sparse and delayed rewards.
- Discount factor:
- When the model available to the agent is estimated from data, the policy found using a shorter planning horizon can actually be better than a policy learned with the true horizon. On the one hand, artificially reducing the planning horizon leads to a bias since the objective function is modified. However, if a long planning horizon is targeted (the discount factor $\gamma$ is close to 1), there is a higher risk of overfitting. This can intuitively be understood as linked to the accumulation of the errors in the transitions and rewards estimated from data as compared to the actual transition and reward probabilities.
- A high discount factor also requires specific care in value iteration algorithms as it can lead to instabilities in convergence. This effect is due to the mappings used in the value iteration algorithms with bootstrapping that propagate errors more strongly with a high discount factor. When bootstrapping is used in a deep RL value iteration algorithm, the risk of instabilities and overestimation of the value function is empirically stronger for a discount factor close to one.
Hierarchical learning: The possibility of learning temporally extended actions (as opposed to atomic actions that last for one time-step) has been formalized under the name of options. The usage of options is an important challenge in RL because it is essential when the task at hand requires working on long time scales while developing generalization capabilities and easier transfer learning between the strategies.
Bias-overfitting tradeoff: For a given algorithmic parameter setting and keeping all other things equal, the right level of complexity is the one at which the increase in bias is equivalent to the reduction of overfitting (or the increase in overfitting is equivalent to the reduction of bias).
- Offline setting:
- Regression-based approach: fit an MDP model to the data via regression (or simply use the frequentist statistics for finite state and action space). The empirical MDP can then be used to evaluate the policy. This purely model-based estimator has alternatives that do not require fitting a model. One possibility is to use a policy evaluation step obtained by generating artificial trajectories from the data, without explicitly referring to a model, thus designing a Model-free Monte Carlo-like (MFMC) estimator.
- Importance sampling approach: use the idea of importance sampling that lets us obtain an estimate of $V ^ { \pi } ( s )$ from trajectories that come from a behavior policy $\beta \neq \pi$ , where $\beta$ is assumed to be known. That approach is unbiased but the variance usually grows exponentially in horizon, which renders the method unsuitable when the amount of data is low.
- Mix of the regression-based approach and the importance sampling approach: use a doubly-robust estimator that is both unbiased and with a lower variance than the importance sampling estimators.
- Online setting: A performant policy from given data is part of the solution to an efficient exploration/exploitation tradeoff. For that reason, progressively fitting a function approximator as more data becomes available can in fact be understood as a way to obtain a good bias-overfitting tradeoff throughout learning. With the same logic, progressively increasing the discount factor allows optimizing the bias-overfitting tradeoff through learning. Besides, optimizing the bias-overfitting tradeoff also suggests the possibility to dynamically adapt the feature space and/or the function approximator.
Challenges in the online setting
In the online setting, two specific elements have not yet been discussed in depth. First, the agent can influence how to gather experience so that it is the most useful for learning. Second, the agent has the possibility to use a replay memory that allows for a good data-efficiency.
Exploration/Exploitation dilemma: Exploration is about obtaining information about the environment (transition model and reward function) while exploitation is about maximizing the expected return given the current knowledge. As an agent starts accumulating knowledge about its environment, it has to make a tradeoff between learning more about its environment (exploration) or pursuing what seems to be the most promising strategy with the experience gathered so far (exploitation).
-
Different settings in the exploration/exploitation dilemma:
- First setting: The agent is expected to perform well without a separate training phase. Thus, an explicit tradeoff between exploration versus exploitation appears so that the agent should explore only when the learning opportunities are valuable enough for the future to compensate what direct exploitation can provide. The sub-optimality $\underset { s _ { 0 } } { \mathbb { E } } [ V ^ { * } ( s _ { 0 } ) - V ^ { \pi } ( s _ { 0 } ) ]$ of an algorithm obtained in this context is known as the cumulative regret.
- Common setting: The agent is allowed to follow a training policy during a first phase of interactions with the environment so as to accumulate training data and hence learn a test policy. In the training phase, exploration is only constrained by the interactions it can make with the environment (e.g., a given number of interactions). The test policy should then be able to maximize a cumulative sum of rewards in a separate phase of interaction. The sub-optimality $\underset { s _ { 0 } } { \mathbb { E } } [ V ^ { * } ( s _ { 0 } ) - V ^ { \pi } ( s _ { 0 } ) ]$ obtained in this case of setting is known as the simple regret. Note that an implicit exploration/exploitation is still important. The agent has to ensure that the lesser-known parts of the environment are not promising (exploration). And the agent is interested in gathering experience in the most promising parts of the environment (which relates to exploitation) to refine the knowledge of the dynamics.
-
Approaches to exploration:
- Directed exploration: The agent makes use of a memory of the past interactions with the environment. For MDPs, directed exploration can scale polynomially with the size of the state space while undirected exploration scales in general exponentially with the size of the state space. Inspired by the Bayesian setting, directed exploration can be done via heuristics of exploration bonus or by maximizing Shannon information gains. The key challenge for directed exploration is to handle, for high-dimensional spaces, the exploration/exploitation tradeoff in a principled way – with the idea to encourage the exploration of the environment where the uncertainty due to limited data is the highest. When rewards are not sparse, a measure of the uncertainty on the value function can be used to drive the exploration. When rewards are sparse, this is even more challenging and exploration should in addition be driven by some novelty measures on the observations (or states in a Markov setting).
- Undirected exploration: The agent does not rely on any exploration specific knowledge of the environment, such as $\epsilon$-greedy and softmax exploration (also called Boltzmann exploration) which takes an action with a probability that depends on the associated expected return.
Managing experience replay
-
In online learning, the agent has the possibility to use a replay memory that allows for data-efficiency by storing the past experience of the agent in order to have the opportunity to reprocess it later. In addition, a replay memory also ensures that the mini-batch updates are done from a reasonably stable data distribution kept in the replay memory which helps for convergence/stability. In an online setting, the replay memory keeps all information for the last $N _{replay} \in N$ time steps, where $N _{replay}$ is constrained by the amount of memory available.
-
While a replay memory allows processing the transitions in a different order than they are experienced, there is also the possibility to use prioritized replay. This allows for consideration of the transitions with a different frequency than they are experienced depending on their significance (that could be which experience to store and which ones to replay). A disadvantage of prioritized replay is that, in general, it also introduces a bias; indeed, by modifying the apparent probabilities of transitions and rewards, the expected return gets biased. Note that this bias can be partly or completely corrected using weighted importance sampling, and this correction is important near convergence at the end of training.
Beyond MDPs
Partial observability and the distribution of (related) MDPs: In both two settings, at each step in the sequential decision process, the agent may benefit from taking into account its whole observable history up to the current time step $t$ when deciding what action to perform. In other words, a history of observations can be used as a pseudo-state (pseudo-state because that refers to a different and abstract stochastic control process). Any missing information in the history of observations (potentially long before time $t$) can introduce a bias in the RL algorithm.
The partially observable scenario
- Partially Observable Markov Decision Process (POMDP): A POMDP is a 7-tuple ($S, A, T, R, \Omega, O, \gamma$) where:
- $S$ is a finite set of states ${1, \cdots , N _ S}$,
- $A$ is a finite set of actions ${1, \cdots , N _ A}$,
- $P: S \times A \times S \rightarrow [0, 1]$ is the transition function,
- $R: S \times A \times S \rightarrow R$ is the reward function, where $R$ is a continuous set of possible rewards in a range $R _ {max} \in R ^ {+}$,
- $\Omega$ is a finite set of observations ${1, \cdots , N _ {\Omega}}$,
- $O: S \times \Omega \rightarrow [0, 1]$ is a set of conditional observation probabilities,
- $\gamma \in [0,1)$ is the discount factor.
- The environment starts in a distribution of initial states $b(s _ 0)$. At each time step $t \in \mathbb{N} _ {0}$, the environment is in a state $s _ {t} \in S$. At the same time, the agent receives an observation $\omega _ {t} \in \Omega$ that depends on the state of the environment with probability $O(s _ {t}, {\omega} _ {t})$, after which the agent chooses an action $a _ {t} \in A$. Then, the environment transitions to state $s _ {t+1} \in S$ with probability $P(s _ {t}, a _ {t}, s _ {t+1})$ and the agent receives a reward $r _ {t} \in R$ equal to $R(s _ {t}, a _ {t}, s _ {t+1})$.
- When the full model ($P$, $R$ and $O$) are known, methods such as Point-Based Value Iteration (PBVI) algorithm for POMDP planning can be used to solve the problem.
- We denote by $H _ { t } = \Omega \times ( A \times R \times \Omega ) ^ { t }$ the set of histories observed up to time $t$ for $t \in {N _ 0}$, and by $H = \bigcup _ { t = 0 } ^ { \infty } H _ { t }$ the space of all possible observable histories.
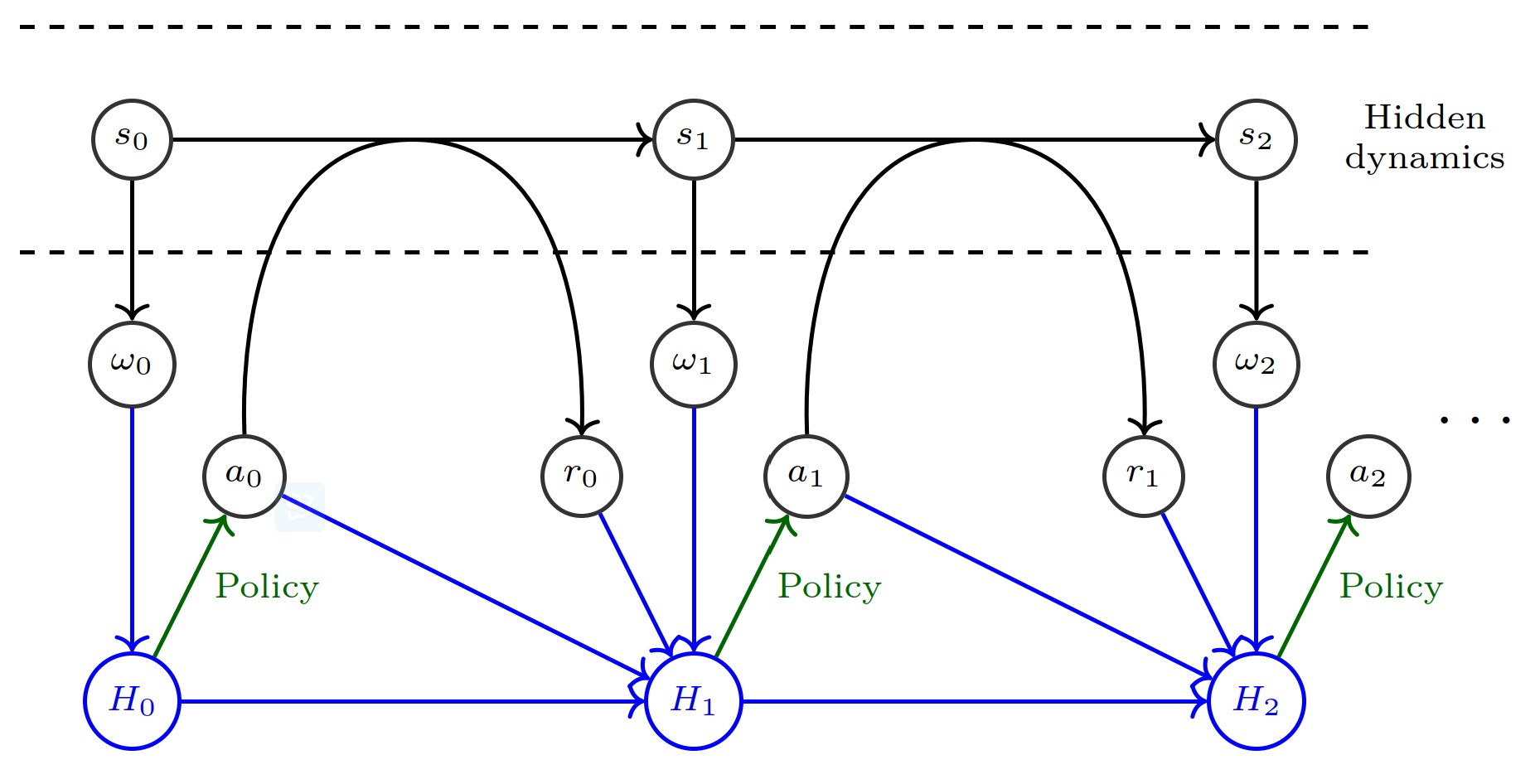
- Architectures such as convolutional layers or recurrency are particularly well-suited to deal with a large input space because they offer interesting generalization properties. A few empirical successes on large scale POMDPs make use of convolutional layers and/or recurrent layers, such as LSTMs.
The distribution of (related) environments
-
In this setting, the environment of the agent is a distribution of different (yet related) tasks that differ for instance in the reward function or in the probabilities of transitions from one state to another. Each task $T _ {i} \sim T$ can be defined by the observations $\omega _ {t} \in \Omega$ (which are equal to $s _ {t}$ if the environments are Markov), the rewards $r _ {t} \in R$, as well as the effect of the actions $a _ {t} \in A$ taken at each step. Similarly to the partially observable context, we denote the history of observations by $H _ {t}$, where $H _ { t } \in H _ { t } = \Omega \times ( A \times R \times \Omega ) ^ { t }$. The agent aims at finding a policy $\pi ( a _ { t } | H _ { t } ; \theta )$ with the objective of maximizing its expected return, defined (in the discounted setting) as $$\underset { T _ { i } \sim \mathcal { T } } { \mathbb { E } } [ \sum _ { k = 0 } ^ { \infty } \gamma ^ { k } r _ { t + k } | H _ { t } , \pi ]$$
-
Different approaches have been investigated in the literature. The Bayesian approach aims at explicitly modeling the distribution of the different environments, if a prior is available. However, it is often intractable to compute the Bayesian-optimal strategy and one has to rely on more practical approaches that do not require an explicit model of the distribution. The concept of meta-learning or learning to learn aims at discovering, from experience, how to behave in a range of tasks and how to negotiate the exploration-exploitation tradeoff. Some other approaches have also been investigated. One possibility is to train a neural network to imitate the behavior of known optimal policies on MDPs drawn from the distribution. The parameters of the model can also be explicitly trained such that a small number of gradient steps in a new task from the distribution will produce fast learning on that task.
Transfer learning
- Zero-shot learning: The idea of zero-shot learning is that an agent should be able to act appropriately in a new task directly from experience acquired on other similar tasks. To achieve this, the agent must either (i) develop generalization capacities described or (ii) use specific transfer strategies that explicitly retrain or replace some of its components to adjust to new tasks. The underlying reason for these successes is the ability of the deep learning architecture to generalize between states that have similar high-level representations and should therefore have the same value function/policy in different domains. Another approach to zero-shot transfer is to use algorithms that enforce states that relate to the same underlying task but have different renderings to be mapped into an abstract state that is close. To develop generalization capacities, one approach is to use an idea similar to data augmentation in supervised learning so as to make sense of variations that were not encountered in the training data.
- Lifelong learning or continual learning: lifelong machine learning relates to the capability of a system to learn many tasks over a lifetime from one or more domains. In general, deep learning architectures can generalize knowledge across multiple tasks by sharing network parameters. A direct approach is thus to train function approximators (e.g. policy, value function, model, etc.) sequentially in different environments. The difficulty of this approach is to find methods that enable the agent to retain knowledge in order to more efficiently learn new tasks. The problem of retaining knowledge in deep reinforcement learning is complicated by the phenomenon of catastrophic forgetting, where generalization to previously seen data is lost at later stages of learning. The straightforward approach is to either (i) use experience replay from all previous experience, or (ii) retrain occasionally on previous tasks similar to the meta-learning setting. When these two options are not available, or as a complement to the two previous approaches, one can use deep learning techniques that are robust to forgetting, such as progressive networks. The idea is to leverage prior knowledge by adding, for each new task, lateral connections to previously learned features (that are kept fixed). Other approaches to limiting catastrophic forgetting include slowing down learning on the weights important for previous tasks and decomposing learning into skill hierarchies.
- Curriculum learning: the goal of curriculum learning is to explicitly design a sequence of source tasks for an agent to train on such that the final performance or learning speed is improved on a target task. The idea is to start by learning small and easy aspects of the target task and then to gradually increase the difficulty level.
Learning without explicit reward function
Due to the complexity of environments in practical applications, defining a reward function can turn out to be rather complicated. There are two other possibilities: (i) given demonstrations of the desired task, we can use imitation learning or extract a reward function using inverse reinforcement learning; (ii) a human may provide feedback on the agent’s behavior in order to define the task.
-
Learning from demonstrations: Given an observed behavior (e.g. the trajectories of an expert/teacher agent), the goal is to have the agent perform similarly. Two approaches are possible:
- Imitation learning uses supervised learning to map states to actions from the observations of the expert’s behavior.
- Inverse reinforcement learning (IRL) determines a possible reward function given observations of optimal behavior. For example, let us consider a large MDP for which the expert always ends up transitioning to the same state. In that context, one may be able to easily infer, from only a few trajectories, what the probable goal of the task is (a reward function that explains the behavior of the teacher), as opposed to directly learning the policy via imitation learning, which is much less efficient.
- Another setting requires the agent to learn directly from a sequence of observations without corresponding actions (and possibly in a slightly different context). This may be done in a meta-learning setting by providing positive reward to the agent when it performs as it is expected based on the demonstration of the teacher. The agent can then act based on new unseen trajectories of the teacher, with the objective that is can generalize sufficiently well to perform new tasks.
-
Learning from direct feedback: Learning from feedback investigates how an agent can interactively learn behaviors from a human teacher who provides positive and negative feedback signals. In order to learn complex behavior, human trainer feedbacks has the potential to be more performant than a reward function defined a priori.
-
Multi-agent systems:
- A multi-agent POMDP with $N$ agents is a tuple ($S, A _ { N }, \ldots , A _ { N } , P , R _ { 1 } , \ldots , R _ { N } , \Omega , O _ { 1 } , \ldots , O _ { N } , \gamma$) where:
- S is a finite set of states {$1, \ldots, N _ {S}$} (describing the possible configurations of all agents);
- $A = A _ {1} \times \ldots \times A _ {n}$ is a finite set of actions {$1, \ldots , N _ {A}$};
- $P : S \times A \times S \rightarrow [0, 1]$ is the transition function (set of conditional transition probabilities between states);
- $\forall i , R _ { i } : S \times A _ { i } \times S \rightarrow \mathbb{R}$ is the reward function for agent $i$;
- $\Omega$ is a finite set of observations {$1, \ldots, N _ {\Omega}$};
- $\forall i , O _ { i } : S \times \Omega \rightarrow [0, 1]$ is a set of conditional observation probabilities
- $\gamma \in [0, 1)$ is the discount factor.
- Collaborative versus non-collaborative setting: In a pure collaborative setting, agents have a shared reward measurement ($R _ {i} = R _ {j}, \forall i, j \in [1, \ldots, N]$). In a mixed or non-collaborative (possibly adversarial) setting each agent obtains different rewards. In both cases, each agent $i$ aims to maximize a discounted sum of its rewards $\sum _ { t = 0 } ^ { H } \gamma ^ { t } r _ { t } ^ { ( i ) }$.
- Decentralized versus centralized setting: In a decentralized setting, each agent selects its own action conditioned only on its local information. When collaboration is beneficial, this decentralized setting can lead to the emergence of communication between agents in order to share information. In a centralized setting, the RL algorithm has access to all observations $w ^ {(i)}$ and all rewards $r ^ {(i)}$. The problem can be reduced to a single-agent RL problem on the condition that a single objective can be defined (in a purely collaborative setting, the unique objective is straightforward). Note that even when a centralized approach can be considered (depending on the problem), an architecture that does not make use of the multi-agent structure usually leads to sub-optimal learning.
-
In general, multi-agent systems are challenging because agents are independently updating their policies as learning progresses, and therefore the environment appears non-stationary to any particular agent. For training one particular agent, one approach is to select randomly the policies of all other agents from a pool of previously learned policies. This can stabilize training of the agent that is learning and prevent overfitting to the current policy of the other agents.
Perspectives on deep reinforcement learning
Challenges of applying reinforcement learning to real-world problems: In practice, even in the case where the task is well defined (explicit reward function), there is one fundamental difficulty: it is often not possible to let an agent interact freely and sufficiently in the actual environment (or set of environments), due to either safety, cost or time constraints.
- The agent may not be able to interact with the true environment but only with an inaccurate simulation of it. When first learning in a simulation, the difference with the real-world domain is known as the reality gap.
- The acquisition of new observations may not be possible anymore (e.g. the batch setting). This scenario happens for instance in medical trials, in tasks with dependence on weather conditions or in trading markets (e.g. energy markets and stock markets).
In order to deal with these limitations, different elements are important:
- One can aim to develop a simulator that is as accurate as possible.
- One can design the learning algorithm so as to improve generalization and/or use transfer learning methods.
Relations between deep RL and neuroscience
During the development of algorithms able to solve challenging sequential decision-making tasks, biological plausibility was not a requirement from an engineering standpoint. However, biological intelligence has been a key inspiration for many of the most successful algorithms.
-
Reinforcement: Driven by such connections, many aspects of reinforcement learning have also been investigated directly to explain certain phenomena in the brain. For instance, computational models have been an inspiration to explain cognitive phenomena such as exploration and temporal discounting of rewards. In cognitive science, Kahneman has also described that there is a dichotomy between two modes of thoughts: a “System 1” that is fast and instinctive and a “System 2” that is slower and more logical. In deep reinforcement, a similar dichotomy can be observed when we consider the model-free and the model-based approaches. Indeed, a conscious thought at a particular time instant can be seen as a low-dimensional combination of a few concepts in order to take decisions.
-
Deep learning: Deep learning also finds its origin in models of neural processing in the brain of biological entities. However, subsequent developments are such that deep learning has become partly incompatible with current knowledge of neurobiology. The convolutional structure used in deep learning that is inspired by the organization of the animal visual cortex.